Termin- und Kapazitätsplanung

1. Überblick

Von der Projektablaufplanung (Projektplanung) unterscheidet sich die Termin- und Kapazitätsplanung nur insoweit, als dass auf der vertikalen Achse eines Gantt-Diagrammes nun nicht mehr die Aufgaben, sondern die Aufgabenträger dargestellt sind. Eine Termin- und Kapazitätsplanung liegt vor, wenn

• aus einer Projektablaufplanung ein Maschinenbelegungsplan erstellt wird, der Auskunft darüber geben soll, welche Maschine oder Anlage zu welcher Zeit für welche Aufgabe eingesetzt werden soll, oder

• aus einer Projektablaufplanung ein Personal-Einsatzplan erstellt wird, der Auskunft darüber gibt, wer zu welcher Zeit welche Aufgabe zu erledigen hat (Personal-Controlling, Personalbedarfsermittlung).

Basis der Termin- und der Kapazitätsplanung ist stets die Summe aller für eine Zeit relevanten Netzpläne und Projektablaufpläne. Die Aufstellung der Termin- und Kapazitätsplanung erfordert die simultane Abstimmung aller Teilplanungen und ist daher eher eine Kunst denn ein exaktes Instrumentarium. Kommt es zu Terminänderungen, so haben diese durch die damit verbundenen Änderungen der Maschinen- oder Ressourcenbelegung zumeist auch Einfluss auf andere Projekte, die ansonsten mit dem verzögerten Vorhaben vollkommen unverbunden sind.

Obwohl hierfür exakte mathematische Planungsalgorithmen zur Verfügung stehen, ist es in der Regel für einen kleinen oder mittelständischen Betrieb weder möglich noch praktikabel, solche Verfahren anzuwenden. Vielmehr haben sich in der betrieblichen Praxis bestimmte Faustregeln bewährt:

• Bei der Verzugszeitregel werden die Aufträge mit dem größten zeitlichen Verzug zuerst eingeplant, d. h., es wird zuerst gemacht, was am meisten Verspätung hat. Der Vorteil dieser Variante liegt vor allem im Abbau von Wartezeiten und damit zufriedeneren Kunden. Nachteilig wirkt sich die Überlastung des Produktionsapparates aus, die nach wie vor bestehen bleibt. Häufig ist die Verzugszeitregel eine Reaktion auf unzureichende Kapazitäten und der Versuch, diese temporär zu kaschieren.

• Bei der dynamischen Wertregel bestimmt der Erzeugniswert vor Ausführung des nächsten Produktionsschrittes die Ausführungsreihenfolge. Maßstab können verschiedene betriebliche Maßgrößen sein, insbesondere der anteilige Verkaufspreis oder der erzielte anteilige Deckungsbeitrag. Während der wesentliche Vorteil in der potenziellen Gewinnmaximierung zu sehen ist, besteht der Nachteil dieses Verfahrens darin, dass Billigaufträge liegen bleiben und Kunden verärgert werden.

• Im Rahmen der Leistungsgradregel werden die Aufträge nach Deckungsbeitrag, Reingewinn o. Ä. geordnet ausgeführt. Die Produktionsreihenfolgeplanung nach absoluten Deckungsbeiträgen ist der Grundgedanke der mathematischen Produktionsprogrammoptimierungsmodelle (z. B. Simplex-Verfahren).

• Anwender der FIFO-Regel führen den am längsten wartenden Auftrag als nächstes aus (first-in-first-out). Diese „gerechte“ Reihenfolge (Warteschlangenmodell) ermöglicht eine leichte handels- und steuerrechtliche Bewertung der Zwischenfabrikate und Läger, führt andererseits aber auch dazu, das Eil- oder besonders profitable Aufträge u. U. länger liegen bleiben.

• Bei der Belegungszeitregel haben Aufträge, die am schnellsten ausgeführt werden können, die höchste Priorität, d. h., Großaufträge bleiben zunächst länger liegen. Diese „kompaktere“ Maschinenbelegung kann besonders dann sinnvoll sein, wenn die Gewinnaufschläge bei kleineren Produkten oder Mengen branchenüblich höher sind.

• Ziel der Schlupfzeitregel ist es, die Leerlaufzeiten zwischen den Aufträgen zu verringern, d. h., die Reihenfolgeplanung richtet sich danach, ob die zu einem Auftrag gehörenden Arbeitsschritte in die noch bestehenden zeitlichen Lücken passen. Dies führt einerseits zu einer Optimierung der Auslastung, andererseits bleiben wichtige Aufträge u. U. liegen.

• Bei der Endterminregel wird der Auftrag als nächstes ausgeführt, der als erstes fertig gestellt werden kann. Dies führt zu kurzen Durchlaufzeiten, aber zumeist auch zu einer suboptimalen Maschinenauslastung.

• Anwender der Rüstzeitregel bevorzugen Aufträge mit geringen Rüstzeiten. Dieses Verfahren ist zumeist bei hochspezialisierten, d. h. tiefen Produktionsprogrammen sinnvoller als bei wechselnden Produkten und Produktionsverfahren. Der Vorteil dieser Variante liegt vor allem in der Minimierung der Rüstkosten insbesondere in maschinenintensiven Fertigungsverfahren.

• Bei der externen Prioritätsregel bestimmen Kundenwünsche, Konventionalstrafen, absatzpolitische Erwägungen etc. die Bearbeitungsreihenfolge. Dies führt auf der einen Seite zu einer Minimierung von Ausfallkosten, auf der anderen Seite aber zu Konflikten mit produktionstechnischen Gegebenheiten und damit u. U. zu hohen Rüst- und Wartungskosten. Die externe Prioritätsregel ist zwar marktangepasst, ihr fehlt jedoch jede Gewinn- oder Deckungsbeitragsorientierung. Oftmals ist sie ein nur aus Verlegenheit angewandtes Kriterium.

• Beim Minimization-of-regret wird die Alternative gewählt, die die geringsten negativen Kosten verursacht. Hierzu muss eine Entscheidungsmatrix aufgestellt werden, die die Konsequenzen ausweist, die durch das Unterlassen eines Handelns entstehen würden. Dieses Verfahren stellt das konzeptionell „reinste“ Modell dar. Es ist aber mit einem hohen Rechenaufwand verbunden.

2. Mathematische Methoden der Maschineneinsatzplanung

Aus mathematischer Sicht handelt es sich bei der Maschineneinsatzplanung um ein lineares Optimierungsproblem, bei dem es gilt, eine Zielvariable unter Berücksichtigung linearer Nebenbedingungen zu optimieren. Das optimale Verfahren zur Lösung dieses Problems ist der Simplex-Algorithmus. Alternativ kommen das Gauß’sche Verfahren und die Bestimmung von Lösungen mittels Extremwerten in Frage.

Da die Umsetzung aufwendig ist und mangels Know-how in der Praxis nur selten angewandt wird, soll die Vorgehensweise im Folgenden an einem vereinfachten Beispiel dargestellt werden. Die grundsätzliche Vorgehensweise gliedert sich dabei in folgende Schritte:

• In einem ersten Schritt werden alle möglichen Maschinenbelegungspläne aufgestellt, die die gewählte Projektaufgabe erfüllen.

• Anschließend wird ein Gleichungssystem aufgestellt, das unter Berücksichtigung der Produktionsvarianten die linearen Beschränkungen abbildet.

• Im Schritt 3 wird die Simplex-Basistabelle mithilfe der Dualkonversion aufgestellt.

• Als nächstes wird das Optimierungsproblem durch die Rechenschritte des Simplex-Verfahrens aufgelöst.

• Als letztes werden die Ergebnisse interpretiert.

Zur Anwendung dieses Verfahrens müssen in einem Maschinenbelegungsplan mehrere Produkte oder Projekte simultan vorkommen. Wird nur ein einzelnes Projekt gefahren, so reduziert sich das Problem auf eine Variante des reinen Reihenfolgeproblems (so genanntes „Travelling Salesman Problem“), welches hier nicht näher betrachtet werden soll.

3. Zahlenbeispiel

Ein Hersteller von Haushaltsprodukten bezieht von einem Lieferanten Zellstoffrollen von 80 cm Breite. Daraus sollen mit einem Schneideautomaten folgende Artikel hergestellt werden:

• 7.200 Rollen Toilettenpapier zu 18 cm Breite

• 6.600 Rollen Papierhandtücher zu 30 cm Breite

• 9.100 Küchenrollen zu 40 cm Breite

Aus Vereinfachungsgründen wird jedes einzelne Produkt als Projekt betrachtet. Verschnitt durch den Schneideautomaten soll nicht betrachtet werden. Ermittelt werden soll die minimale Anzahl der einzukaufenden Rollen.

Zur Lösung des Problems werden zunächst alle möglichen Produktionsprogramme aufgestellt. Jedes mögliche Produktionsprogramm entspricht dabei einem Maschinenbelegungsplan. Es sind nur solche Produktionsprogramme zu berücksichtigen, deren Rest (Verschnitt) kleiner als das kleinste Produkt ist.

Mögliche Produktionsprogramme
Produkt	1	2	3	4	5	6
40 cm	2 St	1 St	1 St	0 St	0 St	0 St
30 cm	0 St	1 St	0 St	2 St	1 St	0 St
18 cm	0 St	0 St	2 St	1 St	2 St	4 St
Summe	80 cm	70 cm	76 cm	78 cm	66 cm	72 cm
Rest	0 cm	10 cm	4 cm	2 cm	14 cm	8 cm

Hierbei entspricht jede Spalte einer eingekauften Rolle. Jedes Rohprodukt kann an allen drei Endprodukten (Projekten) in unterschiedlichem Maße beteiligt sein. Insgesamt gibt es nur die in Abbildung 1 dargestellten 6 Möglichkeiten.

Jede Spalte entspricht dabei auch einer Handlungsalternative. Eine spezifische Kombination der möglichen Handlungsalternativen ist aufzufinden. Die Kosten aller möglichen Handlungsalternativen sind stets 1, d. h., entsprechen einer eingekauften Rolle. Dieses Ergebnis lässt sich als Ungleichungssystem wie folgt darstellen:

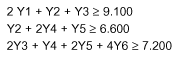
Die Zielfunktion lautet:

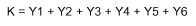
Das Ungleichungssystem lässt sich durch Einfügen von 3 Schlupfvariablen in ein Gleichungssystem überführen:

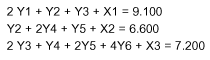
Als Simplex-Basislösung lässt sich dieses Gleichungssystem wie folgt darstellen:

Simplex-Basislösung
	X1	X2	X3	Y1	Y2	Y3	Y4	Y5	Y6	R
Z1	2	0	0	1	0	0	0	0	0	1
Z2	1	1	0	0	1	0	0	0	0	1
Z3	1	0	2	0	0	1	0	0	0	1
Z4	0	2	1	0	0	0	1	0	0	1
Z5	0	1	2	0	0	0	0	1	0	1
Z6	0	0	4	0	0	0	0	0	1	1
Z	-9100	-6600	-7200	0	0	0	0	0	0	0

Die Lösung ist nach drei Iterationen erreicht und sieht folgendermaßen aus:

Lösung
	X1	X2	X3	Y1	Y2	Y3	Y4	Y5	Y6	R
Z1	1	0	0	0,5	0	0	0	0	0	5
Z2	0	0	0	-0,625	1	0,25	-0,5	0	0	0,125
Z3	0	0	1	-0,25	0	0,5	0	0	0	0,25
Z4	0	1	0	0,125	0	-0,25	0,5	0	0	0,375
Z5	0	0	0	0,375	0	-0,75	-0,5	1	0	3125
Z6	0	0	0	1	0	-2	0	0	1	0
Z	0	0	0	3575	0	1950	3300	0	0	8825

Liest man die Lösung nach der bekannten Ableseregel für dualkonvertierte Optimierungsprobleme ab, so erhält man folgendes Ergebnis:

• 3.575 mal Sortiment 1

• 1.950 mal Sortiment 3

• 3.300 mal Sortiment 4

Mit einer kleinen Kontrollrechnung lässt sich überprüfen, ob diese Lösung tatsächlich das gewünschte Ergebnis erbringt:

Kontrollrechnung
Produkt	Soll	1	3	4	Ist-Ergebnis
40 cm	9.100	7.150	1.950	0	9.100 St
30 cm	6.600	0	0	6.600	6.600 St
18 cm	7.200	0	3.900	3.300	7.200 St

Die Mengenwerte in den Spalten „1“, „3“ und „4“ ergeben sich aus der Multiplikation der Produktionsmengen aus der vorstehenden Analyse der möglichen Produktionsprogramme mit der Anzahl der tatsächlich zu fahrenden Sortimente „1“, „3“ und „4“.

Das Ergebnis wird also präzise ohne ein einziges überschüssiges Produkt erreicht. Die optimalen Gesamtkosten betragen 8.825 einzukaufende Rollen, d. h., Kosten einer Rolle multipliziert mit 8.825. Da die Lösung ganzzahlig ist, ist eine Ganzzahligkeitsanalyse entbehrlich.

Insgesamt entspricht dieses Verfahren dem, was man als „zeitgemäße“ Lösung bezeichnen kann. Das Verfahren ist zwar nur mit Softwareunterstützung anwendbar, liefert aber bessere Ergebnisse, als sie mit Faustregeln je erreichbar wären. Diesbezüglich ist noch zu erwähnen, dass sich Beschränkungen des Sortiments etwa durch Konventionalstrafen, extern festgelegte Liefertermine, politisch gewollte Mindestmengen oder staatlich fixierte Zwangspreise als singuläre oder ggf. auch interdependente Restriktionen in das System integrieren lassen.